بعد يعنى چه؟
خوب ما با دو كلمه سر و كار داريم. بعد + چهارم. پس بهتر است كلمه كلمه جلو برويم. اول مفهوم بعد را توضيح مى دهيم.
مى توان بعد را راستا و سمت تعريف كرد. اما نه هر سمتى.هر راستا كه تعريف مى كنيم (و مى توان آن را به شكل يك پيكان نشان داد) بايد بر راستاى قبلى عمود باشد. مثلا اگر ما بگوييم بعد اول، با يك خط صاف طرف هستيم. خطى كه مى توان در آن حركت داشت. يك پيكان دو سو كه مثلا بر حسب جهات اختراعى ما به سمت چپ و راست مى باشد. اين خط را مى توان يك جهان فرض كرد.جهانى 1 بعدى. 1بعدى به معنى وجود يك توانايى حركت. قدرت حركت در يك راستا موجود است .جلو و عقب.
حالا وقتى بخواهيم به اين بعد اول بعد جديدى اضافه كنيم، اين بعد و راستاى جديد بايد حتما بر راستاى قبلى عمود باشد. دقيقا مثل محور مختصات. دنياى يك بعدى مثل محورx است. وقتى مى خواهيم آن را دو بعدى كنيم به آن محور جديد بالا و پايين با نام اختصارى y اضافه مى كنيم.
اين صفحه كه قطر آن صفراست دنياى دو بعدى است.
(جالب: يك كشيش دانا سالها پيش رمانى به نام سطحستان نوشت كه يك چنين دنيايى را تجسم كرده كه در آن اشكال هندسى زندگى مى كنند. مثل مربع و مثلث و دايره. او بيشتر در اين كتاب به محدوديت هاى عصر خود اعتراض كرده بود. ولى روى اين دنياى خيالى و ساده مثال هاى جالبى زده بود كه در هر مثال بحث مهمى از هندسه چهار بعدى نهفته است. از آن به بعد اين بهترين راه براى تحقيق بر بعد چهارم شد. يعنى دانشمند دنياى دو بعدى را مثالى از دنياى ما قرار مى دهد و آنگاه دنياى سه بعدى را مثالى از بعد چهارم مى سازد. آنوقت عقايدش قابل فهم مى شوند. اين كتاب پايه گذارى مهم در اين مبحث به شمار مى رود. )
اگر بعد سومى را بخواهيم بر اين صفحه ى مختصات اضافه كنيم به فضا مى رسيم. براى اين كار راستاى جديدى را بر دو راستاى قبلى اضافه مى كنيم و آن را z مى ناميم. در فضا هر جسمى توانايى حركت در سه بعد را دارد. به سادگى تمام. پس اگر موجودى ساكن اين دنيا باشد آن را سه بعدى خواهيم ناميد.
چهارمین بعد جايى است كه ديگر مغز ما با مشكلاتى در تصور كردن آن مواجه مى شود. شايد باور نكنيد كسانى كه توانايى تصور 4 بعد را داشته اند و شناخته شده اند شايد از انگشتان دست و پاى شما بيشتر نباشند.
حالا به اينجا مى رسيم كه آيا مى شود راستاى جديدى را بر 3 راستاى قبل عمود كرد؟ خوب فكر نمى كنم راهى بيابيد كه چهار چوب را بر هم عمود كنيد. مى دانيد چرا؟ چون ما در دنيايى سه بعدى قرار داريم. همانطور كه در يك صفحه مختصات نمى شود يك مكعب كشيد و بايد حتما اين صفحه را به فضا تبديل كرد، در دنياى ما هم نمى شود چهار چوب را بر هم عمود كرد. اما دنياى چهار بعدى دنيايى است كه در آن مى شود چهار چوب را بر هم عمود كرد. پس اين وسط بعد چهارم مى آيد وسط. ما توانايى حركت در بعد چهارم را نداريم چون سه بعدى هستيم.
![]()
(بعد چهارم و فيزيك: بعضى دانشمندان بنام فيزيك براى كار بر روى نظريات خود به هندسه ى چهار بعدى نيازمند شدند. از آن رو كه مجبور بودند فضا و زمان را با هم پيوند بزنند. از اين رو زمان را راستايى بر جهان سه بعدى ما دانستند. اگر شنيديد بعد چهارم زمان است بدانيد گوينده اشتباهى لفظى كرده است. زمان بعد چهارم است. آن هم به قرارداد فيزيك دانانى كه با فضا زمان سر و كار دارند. اما بعد چهارم ممكن است هر چيزى باشد.در صورتى كه ما درك درستى از هندسه چهار بعدى داشته باشيم در نتيجه درك درستى از فضا زمان داريم. پس مى توانيم اصطلاحاتى مانند خميدگى فضا، فوق كره، آينده و گذشته، كند و تند شدن زمان و ... را بهتر بفهميم.)

۱ نقطه را صفر بعدى مى خوانيم.
۲ نقطه يك خط يك بعدى را تشكيل مى دهد.
۴ خط يك مربع دو بعدى را تشكيل مى دهد.
۶ مربع يك مكعب سه بعدى را تشكيل مى دهد.
۸ مكعب يك فوق مكعب چهار بعدى را نشان مى دهد.
به نوعی می توان این گونه نیز تعبیر کرد
ساختار دو بعدى اى معروف به صليب كه از ۶ مربع تشكيل شده است. با بستن اين ساختار يك مكعب سه بعدى به دست مى آيد. بديهى است كه اين ساختار را نمى توان در جهان دو بعدى كاغذ بست. اين ساختار به مكعب باز شده هم معروف است. البته مكعب بعد از باز شدن مى تواند شكل هاى متفاوت ديگرى هم داشته باشد كه اين معروفترين آنهاست.
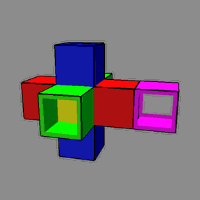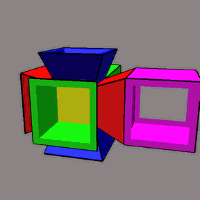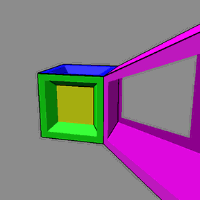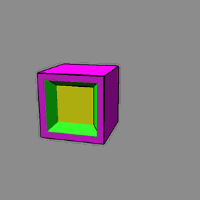
يك ساختار سه بعدى متشكل از ۸ مكعب كه به صليب چهار پر معروف است. اين ساختار در واقع يك فوق مكعب باز شده است. با بستن آن مى توانيم از نو يك فوق مكعب داشته باشيم. ولى مسئله اين است كه اين ساختار در جهان چهار بعدى بسته مى شود.
یک تعریف از ب.4 این است که بگوییم :هر فضایی که شخص با حرکت در جهت عمود به فضای 3 بعدی به آن می رسد فضای چهار بعدی نامیده می شود.
پله اول : بعد صفر

یک نقطه را در داخل فضا تصور کنید.این نقطه یک 0.فوق مکعب است.یک نقطه تنها صفر بعدی است چون نه طول، نه عرض و نه ارتفاع دارد و بینهایت کوچک است.(خیلی به ایدهآل یک انسان در برابر خدا نزدیک شد ).تمام نقطه ها یک اندازه و یکسانند.به این خاطر که آنها بعد ندارند.در زیر تصویر یک نقطه را می بینید که بعد صفر را به ما نشان می دهد.
پله دوم : اولین بعد

این نقطه صفر بعدی را بگیرید و در هر جهتی که دلتان خواست به بیرون بکشید. با این کار یک پاره خط می سازید که همان 1.فوق مکعب است.همه پاره خط ها یک بعد دارند چون فقط در یک مقیاس با هم متفاوت هستند یعنی طول. همه عرض و ارتفاعی برابر دارند که بینهایت بار کوچک است.اگر یک خط را بینهایت بار بکشیم سر تا سر فضای یک بعدی را که در آن قرار دارد پوشش می دهد.
پله سوم : دومین بعد
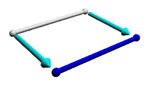
حالا این پاره خط را بگیرید و از قالبش به هر جهتی که نسبت به جهت اول عمود باشد بکشید. یک مربع ساخته خواهد شد که 2.فوق مکعب نامیده می شود. هر مربع دو بعدی به این خاطر که باهم در دو مقیاس متفاوت هستند ، طول و عرض.همه آنها ارتفاع یکسان دارند که بی نهایت بار کوچک است. هر کدام از لبه های این مربع طول یکسان دارند و هر کدام از زوایای آن قائمه هستند.اگر بینهایت بار این مربع را پهن کنید سرتاسر فضای دو بعدی را می پوشاند.
پله چهارم : سومین بعد
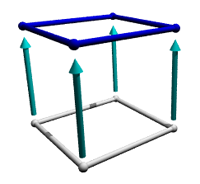
این مربع متناهی را بگیرید و در جهتی که به دو جهت قبلی عمود باشد بکشید و با این کار یک مکعب بسازید که 3.فوق مکعب نامیده می شود.همه مکعب ها سه بعدی هستند به این خاطر که در هر یه مقیاس شناخته شده ما یعنی طول عرض و ارتفاع با هم متفاوتند. درست مانند مربع ، تمام لبه های یک مکعب هم اندازه اند و همه زوایا قائمه هستند.اگر این مکعب را در تمام جهات گسترش دهیم تمام فضای 3 بعدی را پوشش خواهیم داد.
پله پنجم : چهارمین بعد
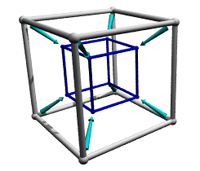
و حالا آخرین مرحله ، یک مکعب محدود را بگیرید و باز هم آن را در جهتی دیگر که بر سه جهت اولیه عمود باشد بیرون بیاورید.
اما چگونه این کار ممکن می شود ؟
این کار در محدودیت های فضای سه بعدی امکان پذیر نیست ( فضایی که در این مقاله به آن فضای حکومتی می گوییم ) اگر چه در فضای چهار بعدی ( که آن را تترا اس پیس می نامیم) این کار امکان پذیر است . شکلی که بواسطه کشش مکعب به داخل تترا اس پیس به دست می آید را تسرکت (tesseract)می نامیم که همان 4.فوق مکعب است.هر تسرکت از لحاظ اندازه در چهار مقیاس با تسرکت های دیگر متفاوت است ( که در یک تسرکت واحد تمام آنها با هم برابر هستند.)
طول ، عرض ، ارتفاع و یک مقیاس چهارم که من آن را تترا طول (trength )می نامم.به مکعب های n بعدی قبلی نگاه کنید، همه آنها تترا طول یکسان و بینهایت کوچک دارند.همچنین درست مانند مکعب و مربع همه لبه ها در یک تسرکت دارای اندازه برابر هستند و همه زوایا قائمه است . اگر یک تسرکت را در همه جهات امتداد دهیم ، همه فضای چهار بعدی را خواهد پوشاند.
روش های گوناگونی برای نشان دادن تسرکت وجود دارد ، که سه تا از این روش ها را در زیر نشان داده میشود.اولین روش تصویر ساری به درون ( افکنش درونی ، تابش به داخل ) است و با استفاده از تصوير پرسپکتيوى یک تسرکت به فضای حکومتی ( فضای 3 بعدی) ساخته می شود. قسمت هایی از تسرکت که دورتر است در تصویر داخلی به صورت کوچکتر ظاهر می شود.چهار چوب اصلی مکعب که قبل از گسترده شدن به تسرکت وجود داشت به رنگ خاکستری ، مسیر رئوس به رنگ سبز (گردن مرغابی) ، و مکان توقف چهار چوب مکعبی گسترده شده به رنگ آبی است.
نکته :تسرکت اصلی شبیه به شکلی که از روش تصویر سازی به درون بدست می آید، نیست در واقع تصورسازی درونی تصویری کاملا تحریف شده از حقیقت یک تسرکت است.
هر کدام از لبه ها که شما در این شکل می بینید در واقع هم اندازه اند و تمام زوایای مابین لبه ها قائمه اند.
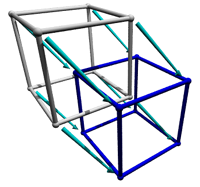
دومین روش برای نشان دان تسرکت باز هم یک تسرکت معمولی نیست و چیزی جز یک تصویر سازی موازی از یک تسرکت اریب نیست.برای ساختن همچین شکلی ابتدا یک چهار چوب مکعبی را تصور کنید سپس چهارچوب مکعب بالائی را در جهتی قطری و به اندازه فاصله کوتاهی در فضای سه بعدی معمولی انتقال دهید .از آنجا که این انتقال موازی و در فضای حکومتی اتفاق می افتد ، در واقع می تواند در هر جهتی که بتوان به سمتش اشاره کرد این انتقال صورت گیرد.بس از انتقال ردی که لبه های تسرکت ایجاد می کند شکل مورد نظر ما را ایجاد میکند.نتیجه این کار شکلی است که دو مکعب با رئوس متصل به هم دارد.در شکل اصلی ، تمام لبه ها در داخل چهار چوب مکعبی اندازه برابر و با هم زاویه قائمه دارند.گرچه ، آنها با لبه های متصل کننده سبز رنگ زاویه قائمه ندارند و این لبه ها اندکی بلند تر از لبه های چهار چوب مکعبی است.

روش سوم برای نشان دان یک تسرکت تصویر سازی موازی است .این روش مانند روش تسرکت مایل است با این تفاوت که دیگر انتقال چهار چوب مکعبی بالا وجود ندارد. از آنچایی که لبه های تسرکت در جهتی که عمود بر فضای حکومتی باشد کشیده می شوند ، زمانی که شکل به داخل خود فضای حکومتی دوباره تصویر می شود لبه های مکعب آبی رنگ بر روی لبه های مکعب خاکستری تصویر می شوند(یعنی یک شکل را در جهتی عمود بر فضای 3 بعدی و دوباره در همان فضای 3بعدی تصویر کنیم) . نتیجه تصویر کردن یک مکعب ساده است.(خلاصه مثل انسان که n تا بعد داره ولی تصویرش همین موجود 3 بعدی زمینی است شاید مثلا بشه ا همین جور یه نظراتی هم راجع به دیدار جبرئیل و پیامبر داد البته فقط نظر).این موضوع در هنگام تصویر سازی درونی اتفاق نیفتاد چون در آنجا ما از اصول پرسپکتیو استفاده میکردیم).
آخرین گام از تلاش برای به تصویر کشیدن یک تسرکت مشکلات نمایش اشیاء فضای چهار بعدی در فضایی که بر ما حکومت می کند با تمام محدودیت هایش نشان داده شد – در واقع یک جهت اضافی وجود دارد که ما قادر به نشان دادن آن بدون تحریف کردن حقیقت شکل اصلی نیستم، به همین دلیل مثال های زیادی برای شروع به درک طبیعت بعد چهارم نیاز است .
فیلم زیر را حتما مشاهده نمایید
http://www.aparat.com/v/ruJkm
:: موضوعات مرتبط:
فیزیک ,
,
|
امتیاز مطلب : 4
|
تعداد امتیازدهندگان : 1
|
مجموع امتیاز : 1
